Barcelona x Chelsea é o confronto com mais chances de acontecer na Champions; veja outras probabilidades
Sorteio da Liga dos Campeões será nesta segunda-feira. Real Madrid, Bayern, Chelsea e Juventus estão no pote 2
Os cruzamentos para a fase de oitavas de final da Champions League serão sorteados na segunda-feira, e nesse ano algumas das probabilidades do sorteio são bem extremas. Por exemplo, o Chelsea só pode enfrentar três equipes: Barcelona, Paris-Saint-Germain e Besiktas. O Chelsea tem 41,3% de possibilidades de jogar contra o Barcelona, e 29,4% de enfrentar PSG e Besiktas.
Os outros possíveis rivais do Barcelona (Basel, Bayern de Munique, Shakhtar Donetsk e Porto) têm quase as mesmas possibilidades de enfrentá-lo (14-15%). Os rivais mais prováveis do Real Madrid são a Roma e o Liverpool, enquanto os do Sevilla são a Roma e o Tottenham (18,9% cada um). Tanto o Real Madrid como o Sevilla têm quase as mesmas probabilidades de enfrentar as duas equipes de Manchester (18,3%). Os cruzamentos menos prováveis de todos são PSG x Porto e Besiktas x Bayern (10,6%). Na tabela seguinte aparecem as probabilidades no sorteio das 16 equipes.
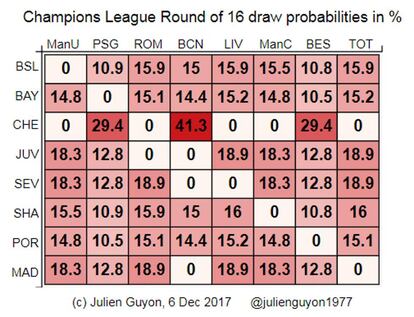
O fato do Barcelona ter tantas probabilidades de jogar contra o Chelsea ocorre pois o Chelsea só pode enfrentar três equipes e o Barcelona, cinco. Como o Chelsea tem tão poucos rivais possíveis? É a consequência das limitações impostas pela UEFA ao sorteio: os ganhadores de grupo devem cruzar com os segundos de grupo; além disso, uma equipe não pode jogar contra outra equipe da mesma confederação (país) assim como contra uma equipe que enfrentou durante a fase de grupos. Nesse ano, excepcionalmente, a Inglaterra conta com cinco representantes na Champions League: os quatro primeiros da Premier League do ano passado, mais o Manchester United, que se classificou ao ganhar a Europa League. Quatro deles ganharam seu grupo: somente o Chelsea acabou em segundo, atrás da Roma. Consequentemente, o Chelsea só pode enfrentar os três vencedores de grupo que não são ingleses (Barcelona, PSG e Besiktas), mas não a Roma.
Seria possível pensar que o Chelsea tem 33,3% de possibilidades de ter alguma dessas três equipes como adversária, e é o que aconteceria se o Chelsea recebesse um tratamento especial no começo do sorteio: se escolheria uma das três bolas (Barcelona, PSG e Besiktas) de um pote para decidir o rival do Chelsea. Mas não é assim que funciona o sorteio.
Também seria possível imaginar que, para calcular a probabilidade que duas equipes A e B têm de se enfrentar, primeiro deve-se fazer uma lista com todos os resultados admissíveis do sorteio, ou seja, os resultados que cumpram todas as limitações (existem 4.238), e depois deve-se calcular a proporção desses 4.238 resultados em que A e B jogam entre si. Entre os 4.238 resultados possíveis do sorteio, existem exatamente 1.854 resultados em que o Chelsea enfrenta o Barcelona, o que equivale a uma proporção de 43,7%, enquanto existem somente 1.192 resultados em que o Chelsea joga com o PSG e o Besiktas (28,1%). A razão pela qual existem mais possibilidades do Chelsea cruzar com o Barcelona é que o Barcelona só pode enfrentar cinco rivais (não pode jogar contra a Juventus, Sevilla e Real Madrid), enquanto o PSG e o Besiktas podem jogar contra sete.
É tentador concluir que a probabilidade de um cruzamento Barcelona x Chelsea é de 43,7%. Seria correto se o sorteio consistisse em colocar 4.238 bolas, uma para cada sorteio possível, em um pote (muito grande) e em escolher uma ao azar para decidir todo o sorteio. Mas, naturalmente, isso não é factível. O sorteio não funciona assim, de modo que o Barcelona e o Chelsea não têm 43,7% de possibilidades de se enfrentarem no sorteio.
Para calcular as probabilidades corretas do sorteio, deve-se analisar o procedimento do sorteio oficial realizado pela UEFA. Nele, esvazia-se por ordem um pote que contém oito bolas, uma para cada segundo de grupo. Cada vez que sai um segundo, um computador enumera os rivais possíveis para cada equipe. Isso pode ser mais complicado do que se pensa. Suponhamos, por exemplo, que os três primeiros confrontos fossem Barcelona x Porto, Tottenham x Basel e PSG x Sevilla. Depois, imaginemos que o Real Madrid é a quarta bola retirada do pote dos segundos. Ainda que a priori possa ser o adversário do Besiktas, o computador consideraria que o Besiktas não é um rival possível para o Real. De fato, colocar o Real Madrid contra os turcos levaria a um beco sem saída: o Chelsea teria então que jogar contra uma equipe inglesa ou contra a Roma, o que é proibido. Quando a lista aparece, um dos grupos possíveis é sorteado ao azar.
Calculei as probabilidades do sorteio simulando o sorteio quatro milhões de vezes, de acordo com o procedimento do sorteio oficial. Na realidade, também é possível calcular as probabilidades exatas em um computador. Os dois métodos dão os mesmos resultados, até o erro de amostragem do método de simulação. O procedimento do sorteio influencia nas probabilidades: um confronto Barcelona x Chelsea é menos provável do que deveria ser (41,3% contra 43,7%), quanto os cruzamentos PSG x Chelsea e Besiktas x Chelsea são mais prováveis do que deveriam ser (29,4% contra 28,1%). O que quero dizer com “deveria ser” é se os 4.238 resultados possíveis do sorteio fossem igualmente prováveis.
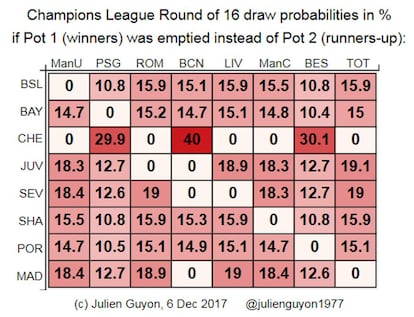
Para mostrar a influência do procedimento nas probabilidades, também calculei quais seriam as probabilidades do sorteio se em vez de esvaziar o pote dos segundos, a UEFA esvaziasse o pote dos vencedores de grupo (usando aqui 400.000 simulações). Sem dúvida, as probabilidades seriam ligeiramente diferentes; por exemplo, a probabilidade de um Barcelona x Chelsea diminuiria para 40%.
Por último, também calculei quais seria as probabilidades do sorteio se o Chelsea tivesse sido o primeiro de seu grupo (1 milhão de simulações). Como podem ver, as probabilidades teriam sido totalmente diferentes não só para o Chelsea, mas para todas as equipes. É surpreendente que o resultado de uma partida tenha tanta influência sobre o restante da competição.
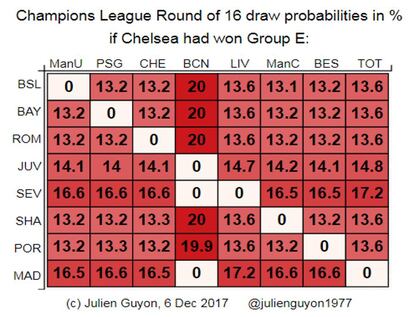
Mas é bom lembrar: o fato de que o Barcelona tem 41,3% de possibilidades de enfrentar o Chelsea também significa que tem mais possibilidades (58,7%) de não enfrentá-lo.
Julien Guyon, matemático francês fã de futebol, é analista de dados e professor adjunto no departamento de Matemática da Universidade de Columbia e no Instituto Courant de Ciências Matemáticas da Universidade de Nova York. Os métodos usados para as simulações estão descritos detalhadamente aqui. Existem mais tabelas de probabilidades disponíveis na conta de Twitter do autor, @julienguyon1977.
