A ordem das operações altera, sim, o resultado: como resolver problemas virais de matemática

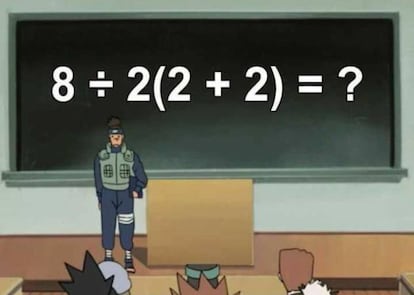
Uma operação aritmética virou de cabeça para baixo o canto sossegado que costuma ser a matemática no Twitter, mas também é uma ótima oportunidade para se falar sobre a ordem das operações. Na aparência, é simples: 8/2 (2 + 2). No entanto, o tuíte original acumula mais de 20.000 respostas em pouco mais de uma semana.

Poderíamos terminar logo: a ordem para realizar as operações é parênteses, potências, multiplicações e divisões e adição e subtração. As conjunções de ligação na sentença anterior estão bem posicionadas. "Multiplicações e divisões" e "adição e subtração" têm a mesma prioridade. Portanto, se você as encontrar juntas, terá que fazê-las da esquerda para a direita, assim como se lê.

Pronto, você já sabe como resolver uma parte importante dos problemas virais no Twitter e no Facebook, aqueles que tentam confundir quem não se lembra de qual é a ordem a seguir nesses casos.

Vamos ver um exemplo que ainda não viralizou nas redes:

3 - 2 + 1 dá um resultado igual a 2, porque se começa da esquerda para a direita, e ninguém vai pensar em adicionar 2 a 1 antes de fazer a diferença, espero, porque seria errado.

No problema que viralizou acontece a mesma coisa:

8 / 2 (2 + 2)

8 / 2 (4)

8 / 2 · 4

4 · 4

16

E então, como foi possível causar tanta polêmica? Bem, porque há uma pequena exceção (e não tem nada a ver com as regras mnemotécnicas PEMDAS ou BODMAS, que explicarei mais abaixo), e é que entre o 2 e o parênteses não há nenhum sinal. Isso é interpretado como uma multiplicação, por isso, ao tirar os parênteses se coloca o ponto, mas, na escrita de expressões algébricas (quando misturamos números e letras), isso poderia ser entendido de outra maneira, especificamente, assim:

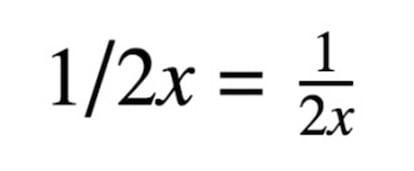
Ou seja, poderíamos interpretar, se isso não fossem números, mas se houvessem letras, que o que aparece à direita da barra divisória é tudo denominador, ou seja:

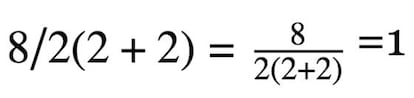
Essa é a razão que levou uma calculadora científica a fornecer esse resultado ao se digitar a operação. Porque ela conduz a operação aritmética como se fosse uma expressão algébrica. Como digo, é a única sutileza desta questão, motivada pela ambiguidade de não se colocar nenhum sinal de pontuação entre o 2 e o parênteses e que geralmente só interpretamos assim em contextos algébricos, não em aritmética.

Por que a ordem das operações importa?

PEMDAS é a sigla em inglês de parênteses, expoentes, multiplicação/divisão, adição/subtração, que é exatamente o que eu já disse. Aqui a multiplicação não tem nenhuma prioridade sobre a divisão, nem tampouco a soma ou adição sobre a subtração. Quando essa regra mnemotécnica é ensinada às crianças de língua inglesa, costuma ser citada a frase “Please Excuse My Dear Aunt Sally”.

Mais informações

O ‘Mary Poppins’ da matemática que se instalava na casa dos colegas para resolver problemas

Karen Uhlenbeck, a pioneira “imperfeita” que levou o ‘Nobel’ de Matemática

Contar com os dedos

BODMAS é a regra mnemotécnica usada pela maioria das crianças inglesas, indianas, bengalis e australianas. Eles representam parênteses (brackets), expoentes (order), divisão/multiplicação, adição/subtração. Como isso de chamar expoentes parece estranho até para eles, às vezes aparece BIDMAS, em que o I vem de índices.

As regras mnemotécnicas são adotadas para ajudar os alunos a lembrar, mas é claro que também são usadas para confundir, já que numerosos artigos publicados desde que apareceu este alvoroço do momento chegaram a acreditar que a ordem em que o M e o D se apresentavam na regra anglo-saxônica da vez tinha influência em se as multiplicações e divisões são feitas ali de forma diferente, e não é assim.

O motivo da ordem em que realizamos as operações ser praticamente o mesmo em todo o mundo é o significado das operações aritméticas. Ou seja, a multiplicação significa “adição reiterada” e, portanto, 5x3 vale 3 + 3 + 3 + 3 + 3 (ou 5 + 5 + 5). Isto implica que quando você vê 3 + 2x5, você deve primeiro calcular o “duas vezes cinco”, porque esse é o seu significado.

O mesmo acontece com a potência, que tem sua origem na multiplicação repetida. Assim, 2x3 ⁴ deve ser entendido como 2 vezes 3 multiplicado por si mesmo quatro vezes. Se você quiser que seja interpretado como seis elevado a 4 (ou multiplicado por si mesmo quatro vezes), você deve colocar um parêntese, (2x3)⁴.

É por tudo isso que a primeira coisa que deve ser abordada são os parênteses, porque eles significam que quem escreveu a operação queria alterar a ordem "natural" das operações. Depois, os expoentes, e então as multiplicações (e divisões, que nada mais são do que suas operações inversas) e as adições (e subtrações, que são suas operações inversas).

Quando eu digo no parágrafo anterior "operações inversas" quero dizer que a subtração é uma "soma disfarçada" e que me perguntar 8-5 é equivalente a me perguntar qual o número que adicionado a 5 dá 8, ou seja, 5 + x = 8. Ocorre o mesmo com a divisão 12: 4, que é equivalente a "qual número multiplicado por 4 dá 12?" É por isso que multiplicação e divisão, adição e subtração, têm a mesma ordem de prioridade e, no caso de várias operações consecutivas, são resolvidas da esquerda para a direita.

Para os leitores que ficaram com vontade de saber mais, há este site em que a ordem dos fatores é alterada e se resolve primeiro a divisão! Para conseguir ser capaz de fazer operações de cabeça com fatores menores. Há alguns outros truques e links para praticar a ordem das operações.